Design affotoniskintegreret kredsløb
Fotoniske integrerede kredsløb(PIC) designes ofte ved hjælp af matematiske scripts på grund af vigtigheden af stilængde i interferometre eller andre applikationer, der er følsomme over for stilængde.PICfremstilles ved at mønstre flere lag (typisk 10 til 30) på en wafer, som er sammensat af mange polygonale former, ofte repræsenteret i GDSII-format. Før filen sendes til fotomaskeproducenten, er det stærkt ønskeligt at kunne simulere PIC'en for at verificere designets korrekthed. Simuleringen er opdelt i flere niveauer: det laveste niveau er den tredimensionelle elektromagnetiske (EM) simulering, hvor simuleringen udføres på subbølgelængdeniveau, selvom interaktionerne mellem atomer i materialet håndteres på makroskopisk skala. Typiske metoder inkluderer tredimensionel finite-difference Time-domain (3D FDTD) og eigenmode-ekspansion (EME). Disse metoder er de mest nøjagtige, men er upraktiske for hele PIC-simuleringstiden. Det næste niveau er 2,5-dimensionel EM-simulering, såsom finite-difference beam propagation (FD-BPM). Disse metoder er meget hurtigere, men ofrer en vis nøjagtighed og kan kun håndtere paraksial udbredelse og kan ikke bruges til at simulere resonatorer, for eksempel. Det næste niveau er 2D EM-simulering, såsom 2D FDTD og 2D BPM. Disse er også hurtigere, men har begrænset funktionalitet, da de f.eks. ikke kan simulere polarisationsrotatorer. Et yderligere niveau er transmissions- og/eller spredningsmatrixsimulering. Hver hovedkomponent reduceres til en komponent med input og output, og den tilsluttede bølgeleder reduceres til et faseforskydnings- og dæmpningselement. Disse simuleringer er ekstremt hurtige. Udgangssignalet opnås ved at gange transmissionsmatricen med inputsignalet. Spredningsmatricen (hvis elementer kaldes S-parametre) multiplicerer input- og outputsignalerne på den ene side for at finde input- og outputsignalerne på den anden side af komponenten. Grundlæggende indeholder spredningsmatricen refleksionen inde i elementet. Spredningsmatricen er normalt dobbelt så stor som transmissionsmatricen i hver dimension. Kort sagt, fra 3D EM til transmissions-/spredningsmatrixsimulering præsenterer hvert lag af simuleringen en afvejning mellem hastighed og nøjagtighed, og designere vælger det rigtige simuleringsniveau til deres specifikke behov for at optimere designvalideringsprocessen.
Det er dog ikke garanteret et fuldstændig korrekt design foran flowpladen at stole på elektromagnetisk simulering af visse elementer og bruge en sprednings-/overføringsmatrix til at simulere hele PIC'en. For eksempel vil fejlberegnede vejlængder, multimode-bølgeledere, der ikke effektivt undertrykker højere ordens modes, eller to bølgeledere, der er for tæt på hinanden, hvilket fører til uventede koblingsproblemer, sandsynligvis ikke blive opdaget under simuleringen. Selvom avancerede simuleringsværktøjer giver effektive designvalideringsmuligheder, kræver det derfor stadig en høj grad af årvågenhed og omhyggelig inspektion fra designeren, kombineret med praktisk erfaring og teknisk viden, for at sikre designets nøjagtighed og pålidelighed og reducere risikoen for flowdiagrammet.
En teknik kaldet sparse FDTD gør det muligt at udføre 3D- og 2D FDTD-simuleringer direkte på et komplet PIC-design for at validere designet. Selvom det er vanskeligt for ethvert elektromagnetisk simuleringsværktøj at simulere en PIC i meget stor skala, er sparse FDTD i stand til at simulere et forholdsvis stort lokalt område. I traditionel 3D FDTD begynder simuleringen ved at initialisere de seks komponenter i det elektromagnetiske felt inden for et specifikt kvantiseret volumen. Efterhånden som tiden går, beregnes den nye feltkomponent i volumenet, og så videre. Hvert trin kræver en masse beregning, så det tager lang tid. I sparse 3D FDTD vedligeholdes en liste over feltkomponenter, der teoretisk kan svare til et vilkårligt stort volumen, og som kun beregnes for disse komponenter, i stedet for at beregne ved hvert trin på hvert punkt i volumenet. Ved hvert tidstrin tilføjes punkter, der støder op til feltkomponenter, mens feltkomponenter under en bestemt effekttærskel udelades. For nogle strukturer kan denne beregning være flere størrelsesordener hurtigere end traditionel 3D FDTD. Sparsomme FDTDS fungerer dog ikke godt, når de håndterer dispersive strukturer, fordi dette tidsfelt spredes for meget, hvilket resulterer i lister, der er for lange og vanskelige at håndtere. Figur 1 viser et eksempel på et skærmbillede af en 3D FDTD-simulering, der ligner en polarisationsstråledeler (PBS).
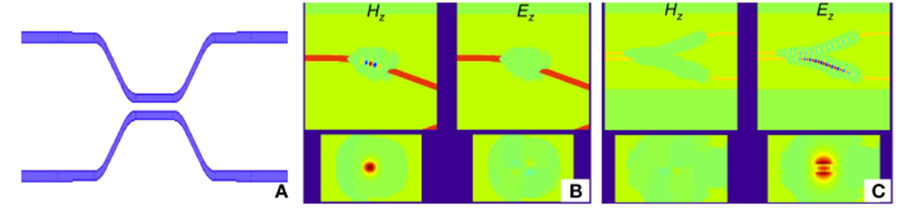
Figur 1: Simuleringsresultater fra 3D sparse FDTD. (A) er en topvisning af den struktur, der simuleres, som er en retningsbestemt kobler. (B) Viser et skærmbillede af en simulering ved hjælp af kvasi-TE-excitation. De to diagrammer ovenfor viser topvisningen af kvasi-TE- og kvasi-TM-signalerne, og de to diagrammer nedenfor viser det tilsvarende tværsnit. (C) Viser et skærmbillede af en simulering ved hjælp af kvasi-TM-excitation.
Opslagstidspunkt: 23. juli 2024





